How Do You Know When a Resistor Is Redundant

Direct-Electric current Circuits

64 Kirchhoff'southward Rules

Learning Objectives

Past the end of the section, you will be able to:

State Kirchhoff's junction rule
State Kirchhoff's loop dominion
Analyze complex circuits using Kirchhoff's rules

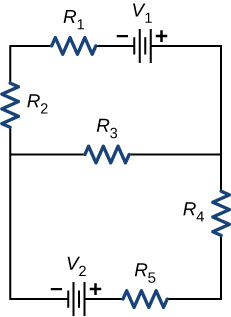
We accept just seen that some circuits may be analyzed by reducing a circuit to a single voltage source and an equivalent resistance. Many circuitous circuits cannot exist analyzed with the series-parallel techniques developed in the preceding sections. In this department, we elaborate on the use of Kirchhoff'south rules to analyze more complex circuits. For example, the excursion in (Figure) is known as a multi-loop circuit, which consists of junctions. A junction, also known as a node, is a connection of three or more wires. In this circuit, the previous methods cannot be used, because not all the resistors are in clear serial or parallel configurations that can be reduced. Give information technology a try. The resistors ${R}_{1}$ and ${R}_{2}$ are in series and can be reduced to an equivalent resistance. The same is true of resistors ${R}_{4}$ and ${R}_{5}$ . But what exercise you practise then?

Fifty-fifty though this circuit cannot be analyzed using the methods already learned, two circuit analysis rules can be used to analyze any circuit, simple or circuitous. The rules are known equally Kirchhoff'south rules, subsequently their inventor Gustav Kirchhoff (1824–1887).

This circuit cannot be reduced to a combination of series and parallel connections. However, we can use Kirchhoff's rules to analyze information technology.

Kirchhoff's Rules

Kirchhoff's kickoff rule—the junction dominion. The sum of all currents entering a junction must equal the sum of all currents leaving the junction:

$\sum {I}_{\text{in}}=\sum {I}_{\text{out}}.$
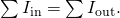
Kirchhoff'south second rule—the loop rule. The algebraic sum of changes in potential around any closed circuit path (loop) must be zero:

$\sum V=0.$

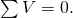
We now provide explanations of these two rules, followed by trouble-solving hints for applying them and a worked example that uses them.

Kirchhoff's Kickoff Rule

Kirchhoff'south first rule (the junction rule) applies to the charge entering and leaving a junction ((Figure)). Every bit stated earlier, a junction, or node, is a connection of three or more wires. Current is the flow of charge, and charge is conserved; thus, whatsoever charge flows into the junction must flow out.

Charge must be conserved, so the sum of currents into a junction must be equal to the sum of currents out of the junction.

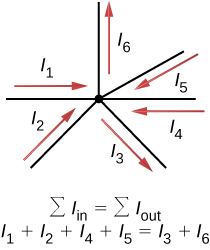
The figure shows a junction with six current branches, four with incoming currents and two with outgoing currents. The sum of incoming currents is equal to sum of outgoing currents.

Although it is an over-simplification, an analogy tin be made with h2o pipes connected in a plumbing junction. If the wires in (Figure) were replaced past h2o pipes, and the water was assumed to be incompressible, the volume of water flowing into the junction must equal the volume of water flowing out of the junction.

Kirchhoff's Second Rule

Kirchhoff's second rule (the loop dominion) applies to potential differences. The loop dominion is stated in terms of potential V rather than potential energy, but the 2 are related since $U=qV.$ In a closed loop, whatever free energy is supplied by a voltage source, the energy must be transferred into other forms past the devices in the loop, since there are no other ways in which free energy can be transferred into or out of the circuit. Kirchhoff's loop rule states that the algebraic sum of potential differences, including voltage supplied by the voltage sources and resistive elements, in any loop must be equal to zero. For example, consider a simple loop with no junctions, equally in (Figure).

A simple loop with no junctions. Kirchhoff's loop rule states that the algebraic sum of the voltage differences is equal to zip.

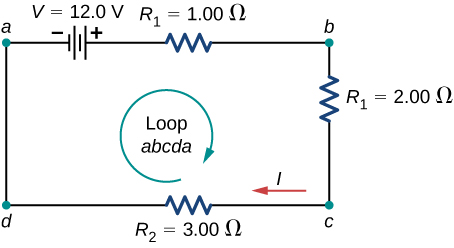
The figure shows a loop with positive terminal of voltage source of 12 V connected to three resistors of 1 Ω, 2 Ω and 3 Ω in series.

The circuit consists of a voltage source and iii external load resistors. The labels a, b, c, and d serve as references, and have no other significance. The usefulness of these labels will get credible before long. The loop is designated as Loop abcda, and the labels help keep track of the voltage differences equally we travel around the circuit. Commencement at betoken a and travel to point b. The voltage of the voltage source is added to the equation and the potential drop of the resistor ${R}_{1}$ is subtracted. From point b to c, the potential drop across ${R}_{2}$ is subtracted. From c to d, the potential drop across ${R}_{3}$ is subtracted. From points d to a, nothing is done because there are no components.

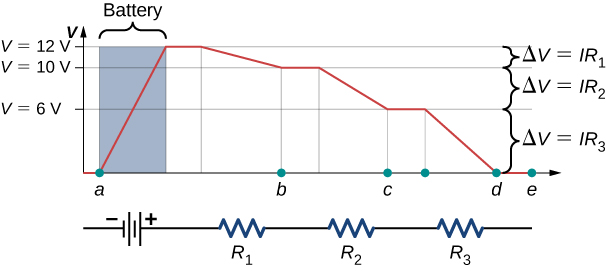
(Figure) shows a graph of the voltage equally we travel around the loop. Voltage increases equally we cantankerous the battery, whereas voltage decreases as we travel beyond a resistor. The potential drib, or change in the electric potential, is equal to the current through the resistor times the resistance of the resistor. Since the wires have negligible resistance, the voltage remains abiding equally we cross the wires connecting the components.

A voltage graph as nosotros travel effectually the excursion. The voltage increases every bit nosotros cross the battery and decreases as we cross each resistor. Since the resistance of the wire is quite small, we assume that the voltage remains abiding every bit we cross the wires connecting the components.

The graph shows voltage at different points of a closed loop circuit with a voltage source and three resistances. The points are shown on x-axis and voltages on y-axis.

Then Kirchhoff's loop dominion states

$V-I{R}_{1}-I{R}_{2}-I{R}_{3}=0.$

The loop equation tin be used to find the current through the loop:

$I=\frac{V}{{R}_{1}+{R}_{2}+{R}_{2}}=\frac{12.00\phantom{\rule{0.2em}{0ex}}\text{V}}{1.00\phantom{\rule{0.2em}{0ex}}\text{Ω}+2.00\phantom{\rule{0.2em}{0ex}}\text{Ω}+3.00\phantom{\rule{0.2em}{0ex}}\text{Ω}}=2.00\phantom{\rule{0.2em}{0ex}}\text{A}.$

This loop could have been analyzed using the previous methods, simply we will demonstrate the ability of Kirchhoff's method in the next section.

Applying Kirchhoff'due south Rules

By applying Kirchhoff's rules, nosotros generate a set of linear equations that allow the states to find the unknown values in circuits. These may exist currents, voltages, or resistances. Each time a rule is applied, information technology produces an equation. If there are as many independent equations every bit unknowns, and then the problem tin be solved.

Using Kirchhoff'southward method of analysis requires several steps, every bit listed in the following procedure.

Trouble-Solving Strategy: Kirchhoff'southward Rules

Label points in the circuit diagram using lowercase letters a, b, c, …. These labels simply help with orientation.
Locate the junctions in the circuit. The junctions are points where 3 or more wires connect. Characterization each junction with the currents and directions into and out of information technology. Make sure at least one current points into the junction and at least one current points out of the junction.
Choose the loops in the circuit. Every component must be contained in at least i loop, but a component may be independent in more than one loop.
Utilise the junction rule. Again, some junctions should not be included in the assay. You need simply use enough nodes to include every electric current.
Use the loop rule. Use the map in (Effigy).

Each of these resistors and voltage sources is traversed from a to b. (a) When moving beyond a resistor in the same direction as the electric current flow, subtract the potential drop. (b) When moving across a resistor in the contrary management every bit the current flow, add the potential drop. (c) When moving across a voltage source from the negative last to the positive terminal, add the potential drop. (d) When moving across a voltage source from the positive final to the negative terminal, decrease the potential drop.

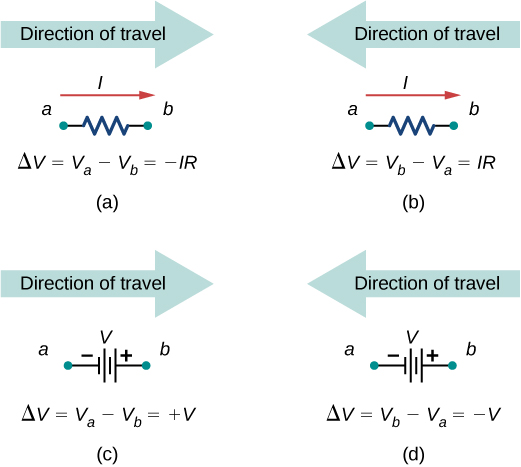
Let's examine some steps in this procedure more closely. When locating the junctions in the excursion, exercise not exist concerned about the management of the currents. If the direction of current flow is non obvious, choosing whatever management is sufficient as long every bit at least 1 current points into the junction and at least one electric current points out of the junction. If the arrow is in the opposite direction of the conventional current menstruum, the result for the electric current in question will be negative but the answer will still exist correct.

The number of nodes depends on the circuit. Each current should exist included in a node and thus included in at to the lowest degree one junction equation. Exercise not include nodes that are not linearly contained, pregnant nodes that incorporate the same data.

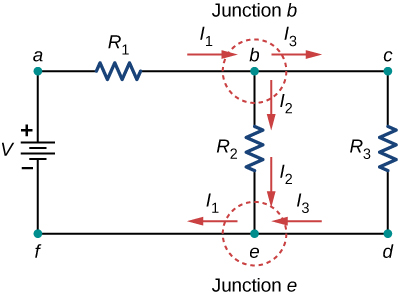
Consider (Figure). At that place are ii junctions in this circuit: Junction b and Junction e. Points a, c, d, and f are non junctions, considering a junction must have iii or more connections. The equation for Junction b is ${I}_{1}={I}_{2}+{I}_{3}$ , and the equation for Junction e is ${I}_{2}+{I}_{3}={I}_{1}$ . These are equivalent equations, so it is necessary to keep only one of them.

At starting time glance, this excursion contains two junctions, Junction b and Junction e, only only i should be considered because their junction equations are equivalent.

The figure shows a circuit with positive terminal of voltage source V connected to resistor R subscript 1 connected to two parallel resistors R subscript 2 and R subscript 3 through junction b. The two resistors are connected to voltage source through junction e.

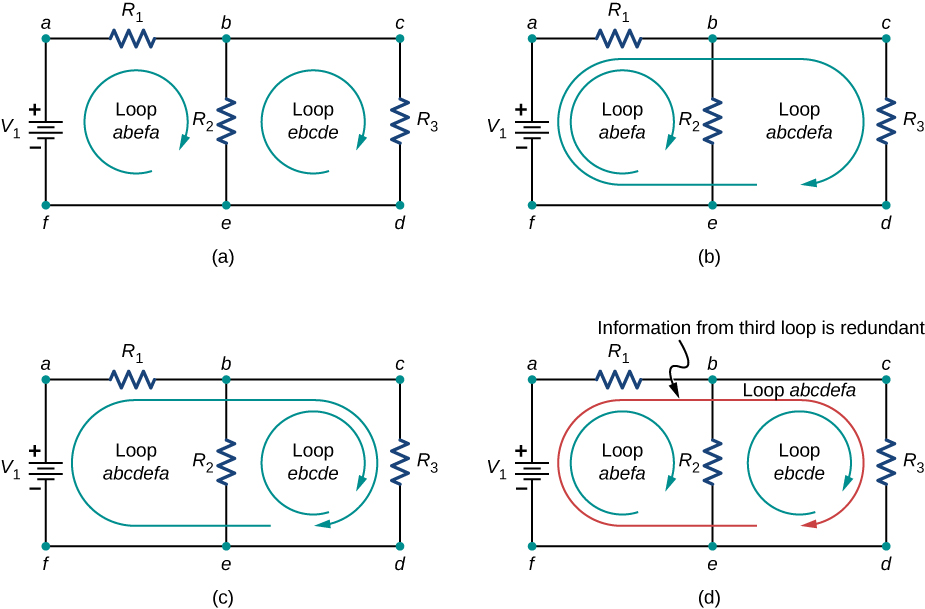
When choosing the loops in the circuit, you need enough loops then that each component is covered in one case, without repeating loops. (Effigy) shows four choices for loops to solve a sample circuit; choices (a), (b), and (c) take a sufficient corporeality of loops to solve the circuit completely. Option (d) reflects more loops than necessary to solve the circuit.

Panels (a)–(c) are sufficient for the analysis of the circuit. In each case, the ii loops shown incorporate all the circuit elements necessary to solve the excursion completely. Console (d) shows three loops used, which is more than necessary. Whatsoever two loops in the arrangement will contain all information needed to solve the circuit. Calculation the third loop provides redundant information.

The figure has four parts showing different loop combinations for a circuit with positive terminal of voltage source V connected to resistor R subscript 1 connected to two parallel resistors R subscript 2 and R subscript 3.

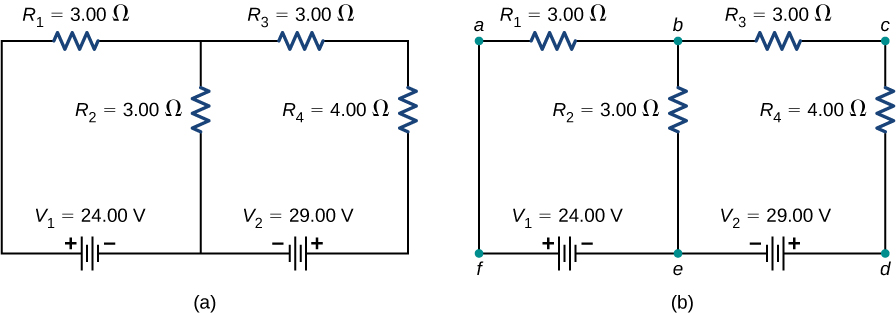
Consider the circuit in (Effigy)(a). Allow us analyze this circuit to detect the current through each resistor. Start, label the excursion equally shown in function (b).

(a) A multi-loop circuit. (b) Characterization the excursion to aid with orientation.

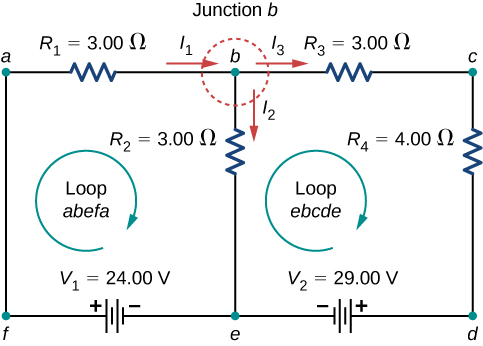
Next, make up one's mind the junctions. In this circuit, points b and e each have 3 wires connected, making them junctions. Start to utilise Kirchhoff'southward junction dominion $\left(\sum {I}_{\text{in}}=\sum {I}_{\text{out}}\right)$ past drawing arrows representing the currents and labeling each arrow, as shown in (Figure)(b). Junction b shows that ${I}_{1}={I}_{2}+{I}_{3}$ and Junction e shows that ${I}_{2}+{I}_{3}={I}_{1}$ . Since Junction e gives the same information of Junction b, it can exist disregarded. This circuit has three unknowns, and then we demand 3 linearly independent equations to analyze it.

(a) This circuit has 2 junctions, labeled b and eastward, but only node b is used in the analysis. (b) Labeled arrows represent the currents into and out of the junctions.

The figure shows positive terminal of voltage source V connected to resistor R subscript 1 connected in series to two parallel resistors, R subscript 2 and R subscript 3.

Next we need to choose the loops. In (Figure), Loop abefa includes the voltage source ${V}_{1}$ and resistors ${R}_{1}$ and ${R}_{2}$ . The loop starts at point a, then travels through points b, eastward, and f, and and so dorsum to point a. The second loop, Loop ebcde, starts at point east and includes resistors ${R}_{2}$ and ${R}_{3}$ , and the voltage source ${V}_{2}$ .

Cull the loops in the circuit.

Now we can apply Kirchhoff's loop rule, using the map in (Figure). Starting at betoken a and moving to point b, the resistor ${R}_{1}$ is crossed in the same direction as the current menstruum ${I}_{1}$ , so the potential drop ${I}_{1}{R}_{1}$ is subtracted. Moving from point b to point e, the resistor ${R}_{2}$ is crossed in the aforementioned direction as the current flow ${I}_{2}$ so the potential drop ${I}_{2}{R}_{2}$ is subtracted. Moving from betoken e to point f, the voltage source ${V}_{1}$ is crossed from the negative final to the positive terminal, so ${V}_{1}$ is added. In that location are no components between points f and a. The sum of the voltage differences must equal zilch:

$\text{Loop}\phantom{\rule{0.2em}{0ex}}abefa:\phantom{\rule{0.5em}{0ex}}-{I}_{1}{R}_{1}-{I}_{2}{R}_{2}+{V}_{1}=0\phantom{\rule{0.2em}{0ex}}\text{or}\phantom{\rule{0.2em}{0ex}}{V}_{1}={I}_{1}{R}_{1}+{I}_{2}{R}_{2}.$

Finally, we check loop ebcde. We start at indicate e and movement to point b, crossing ${R}_{2}$ in the opposite direction as the current menstruum ${I}_{2}$ . The potential driblet ${I}_{2}{R}_{2}$ is added. Adjacent, we cantankerous ${R}_{3}$ and ${R}_{4}$ in the aforementioned direction equally the electric current flow ${I}_{3}$ and subtract the potential drops ${I}_{3}{R}_{3}$ and ${I}_{3}{R}_{4}.$ Note that the current is the same through resistors ${R}_{3}$ and ${R}_{4}$ , because they are connected in series. Finally, the voltage source is crossed from the positive final to the negative concluding, and the voltage source ${V}_{2}$ is subtracted. The sum of these voltage differences equals cipher and yields the loop equation

$\text{Loop}\phantom{\rule{0.2em}{0ex}}ebcde:{I}_{2}{R}_{2}-{I}_{3}\left({R}_{3}+{R}_{4}\right)-{V}_{2}=0.$

Nosotros now have 3 equations, which we can solve for the iii unknowns.

$\begin{array}{}\\ \\ \\ \phantom{\rule{1em}{0ex}}\text{(1)}\phantom{\rule{0.2em}{0ex}}\text{Junction}\phantom{\rule{0.2em}{0ex}}b:{I}_{1}-{I}_{2}-{I}_{3}=0.\hfill \\ \phantom{\rule{1em}{0ex}}\text{(2)}\phantom{\rule{0.2em}{0ex}}\text{Loop}\phantom{\rule{0.2em}{0ex}}abefa:\phantom{\rule{0.5em}{0ex}}{I}_{1}{R}_{1}+{I}_{2}{R}_{2}={V}_{1}.\hfill \\ \phantom{\rule{1em}{0ex}}\text{(3)}\phantom{\rule{0.2em}{0ex}}\text{Loop}\phantom{\rule{0.2em}{0ex}}ebcde:{I}_{2}{R}_{2}-{I}_{3}\left({R}_{3}+{R}_{4}\right)={V}_{2}.\hfill \end{array}$

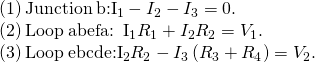
To solve the 3 equations for the three unknown currents, first by eliminating electric current ${I}_{2}$ . Kickoff add Eq. (i) times ${R}_{2}$ to Eq. (2). The event is labeled as Eq. (iv):

$\begin{array}{}\\ \left({R}_{1}+{R}_{2}\right){I}_{1}-{R}_{2}{I}_{3}={V}_{1}.\hfill \\ \\ \\ \phantom{\rule{1em}{0ex}}\text{(4)}\phantom{\rule{0.2em}{0ex}}6\phantom{\rule{0.2em}{0ex}}\text{Ω}{I}_{1}-3\phantom{\rule{0.2em}{0ex}}\text{Ω}{I}_{3}=24\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \end{array}$

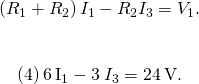
Next, subtract Eq. (iii) from Eq. (two). The issue is labeled as Eq. (five):

$\begin{array}{}\\ {I}_{1}{R}_{1}+{I}_{3}\left({R}_{3}+{R}_{4}\right)={V}_{1}-{V}_{2}.\hfill \\ \\ \\ \phantom{\rule{1em}{0ex}}\text{(5)}\phantom{\rule{0.2em}{0ex}}3\phantom{\rule{0.2em}{0ex}}\text{Ω}{I}_{1}+7\phantom{\rule{0.2em}{0ex}}\text{Ω}{I}_{3}=-5\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \end{array}$

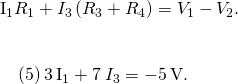
Nosotros tin solve Eqs. (iv) and (5) for electric current ${I}_{1}$ . Calculation vii times Eq. (4) and three times Eq. (5) results in $51\phantom{\rule{0.2em}{0ex}}\text{Ω}{I}_{1}=153\phantom{\rule{0.2em}{0ex}}\text{V},$ or ${I}_{1}=3.00\phantom{\rule{0.2em}{0ex}}\text{A}.$ Using Eq. (4) results in ${I}_{3}=-2.00\phantom{\rule{0.2em}{0ex}}\text{A}.$ Finally, Eq. (1) yields ${I}_{2}={I}_{1}-{I}_{3}=5.00\phantom{\rule{0.2em}{0ex}}\text{A}.$ One way to check that the solutions are consistent is to bank check the ability supplied by the voltage sources and the power prodigal by the resistors:

$\begin{array}{c}{P}_{\text{in}}={I}_{1}{V}_{1}+{I}_{3}{V}_{2}=130\phantom{\rule{0.2em}{0ex}}\text{W},\hfill \\ {P}_{\text{out}}={I}_{1}^{2}{R}_{1}+{I}_{2}^{2}{R}_{2}+{I}_{3}^{2}{R}_{3}+{I}_{3}^{2}{R}_{4}=130\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \end{array}$

Note that the solution for the electric current ${I}_{3}$ is negative. This is the right answer, just suggests that the arrow originally drawn in the junction analysis is the direction opposite of conventional electric current flow. The power supplied by the second voltage source is 58 W and non −58 W.

Calculating Electric current by Using Kirchhoff'south Rules Find the currents flowing in the excursion in (Figure).

This circuit is combination of series and parallel configurations of resistors and voltage sources. This circuit cannot be analyzed using the techniques discussed in Electromotive Force but tin be analyzed using Kirchhoff's rules.

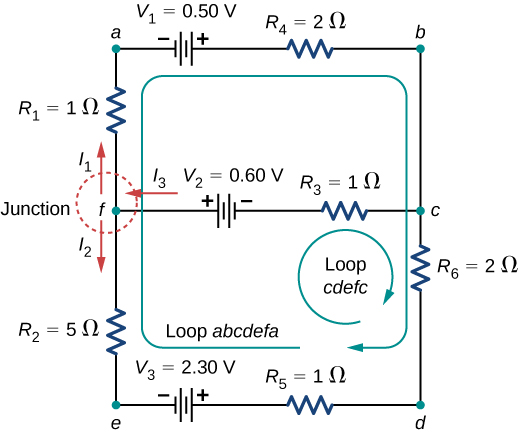
Strategy This circuit is sufficiently complex that the currents cannot exist found using Ohm'southward constabulary and the series-parallel techniques—information technology is necessary to use Kirchhoff's rules. Currents have been labeled ${I}_{1},$ ${I}_{2},$ and ${I}_{3}$ in the figure, and assumptions accept been made about their directions. Locations on the diagram have been labeled with letters a through h. In the solution, nosotros apply the junction and loop rules, seeking three independent equations to allow us to solve for the 3 unknown currents.

Solution Applying the junction and loop rules yields the following three equations. We have three unknowns, then three equations are required.

$\begin{array}{c}\text{Junction}\phantom{\rule{0.2em}{0ex}}c:\phantom{\rule{0.2em}{0ex}}{I}_{1}+{I}_{2}={I}_{3}.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}abcdefa:\phantom{\rule{0.2em}{0ex}}{I}_{1}\left({R}_{1}+{R}_{4}\right)-{I}_{2}\left({R}_{2}+{R}_{5}+{R}_{6}\right)={V}_{1}-{V}_{3}.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}cdefc:\phantom{\rule{0.2em}{0ex}}{I}_{2}\left({R}_{2}+{R}_{5}+{R}_{6}\right)+{I}_{3}{R}_{3}={V}_{2}+{V}_{3}.\hfill \end{array}$

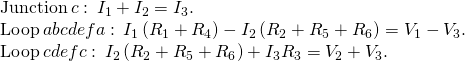
Simplify the equations by placing the unknowns on one side of the equations.

$\begin{array}{c}\text{Junction}\phantom{\rule{0.2em}{0ex}}c:\phantom{\rule{0.2em}{0ex}}{I}_{1}+{I}_{2}-{I}_{3}=0.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}abcdefa:\phantom{\rule{0.2em}{0ex}}{I}_{1}\left(3\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)-{I}_{2}\left(8\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=0.5\phantom{\rule{0.2em}{0ex}}\text{V}-2.30\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}cdefc:\phantom{\rule{0.2em}{0ex}}{I}_{2}\left(8\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)+{I}_{3}\left(1\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=0.6\phantom{\rule{0.2em}{0ex}}\text{V}+2.30\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \end{array}$

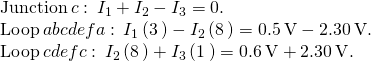
Simplify the equations. The first loop equation tin can be simplified by dividing both sides past 3.00. The second loop equation can be simplified past dividing both sides past 6.00.

$\begin{array}{c}\text{Junction}\phantom{\rule{0.2em}{0ex}}c:\phantom{\rule{0.2em}{0ex}}{I}_{1}+{I}_{2}-{I}_{3}=0.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}abcdefa:\phantom{\rule{0.2em}{0ex}}{I}_{1}\left(3\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)-{I}_{2}\left(8\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=\text{−}1.8\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \\ \text{Loop}\phantom{\rule{0.2em}{0ex}}cdefc:\phantom{\rule{0.2em}{0ex}}{I}_{2}\left(8\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)+{I}_{3}\left(1\phantom{\rule{0.2em}{0ex}}\text{Ω}\right)=2.9\phantom{\rule{0.2em}{0ex}}\text{V}.\hfill \end{array}$

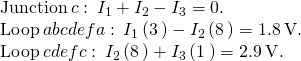
The results are

${I}_{1}=0.20\phantom{\rule{0.2em}{0ex}}\text{A},\phantom{\rule{0.5em}{0ex}}{I}_{2}=0.30\phantom{\rule{0.2em}{0ex}}\text{A},\phantom{\rule{0.5em}{0ex}}{I}_{3}=0.50\phantom{\rule{0.2em}{0ex}}\text{A}.$

Significance A method to check the calculations is to compute the power prodigal by the resistors and the power supplied past the voltage sources:

$\begin{array}{}\\ {P}_{{R}_{1}}={I}_{1}^{2}{R}_{1}=0.04\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{{R}_{2}}={I}_{2}^{2}{R}_{2}=0.45\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{{R}_{3}}={I}_{3}^{2}{R}_{3}=0.25\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{{R}_{4}}={I}_{1}^{2}{R}_{4}=0.08\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{{R}_{5}}={I}_{2}^{2}{R}_{5}=0.09\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{{R}_{6}}={I}_{2}^{2}{R}_{6}=0.18\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{\text{dissipated}}=1.09\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \\ {P}_{\text{source}}={I}_{1}{V}_{1}+{I}_{2}{V}_{3}+{I}_{3}{V}_{2}=0.10\phantom{\rule{0.2em}{0ex}}\text{W}+0.69\phantom{\rule{0.2em}{0ex}}\text{W}+0.30\phantom{\rule{0.2em}{0ex}}\text{W}=1.09\phantom{\rule{0.2em}{0ex}}\text{W}.\hfill \end{array}$

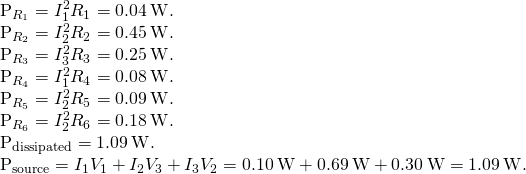
The ability supplied equals the power dissipated by the resistors.

Check Your Understanding In because the following schematic and the power supplied and consumed by a circuit, will a voltage source always provide ability to the circuit, or tin a voltage source swallow ability?

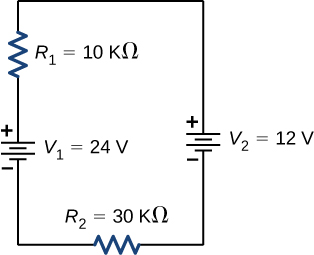
The figure shows positive terminal of voltage source V subscript 1 of 24 V connected in series to resistor R subscript 1 of 10 kΩ connected in series to positive terminal of voltage source V subscript 2 of 12 V connected in series to resistor R subscript 2 of 30 kΩ.

The circuit tin be analyzed using Kirchhoff's loop rule. The commencement voltage source supplies power: ${P}_{\text{in}}=I{V}_{1}=7.20\phantom{\rule{0.2em}{0ex}}\text{mW.}$ The 2nd voltage source consumes ability: ${P}_{\text{out}}=I{V}_{2}+{I}^{2}{R}_{1}+{I}^{2}{R}_{2}=7.2\phantom{\rule{0.2em}{0ex}}\text{mW}.$

Calculating Electric current by Using Kirchhoff's Rules Find the current flowing in the circuit in (Figure).

This circuit consists of three resistors and two batteries continued in series. Note that the batteries are connected with contrary polarities.

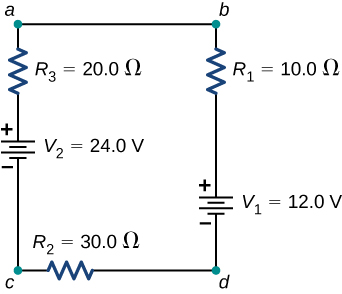
The figure shows positive terminal of voltage source V subscript 2 of 24 V connected in series to resistor R subscript 3 of 20 Ω connected in series to resistor R subscript 1 of 10 Ω connected in series to positive terminal of voltage source V subscript 1 of 12 V connected in series to resistor R subscript 2 of 30 Ω.

Strategy This excursion tin exist analyzed using Kirchhoff's rules. There is only i loop and no nodes. Choose the management of current menstruum. For this case, we volition use the clockwise management from betoken a to point b. Consider Loop abcda and use (Figure) to write the loop equation. Note that according to (Figure), battery ${V}_{1}$ will exist added and battery ${V}_{2}$ will exist subtracted.

Solution Applying the junction rule yields the post-obit three equations. We take one unknown, so ane equation is required:

$\text{Loop}\phantom{\rule{0.2em}{0ex}}abcda:\phantom{\rule{0.2em}{0ex}}-I{R}_{1}-{V}_{1}-I{R}_{2}+{V}_{2}-I{R}_{3}=0.$

Simplify the equations by placing the unknowns on i side of the equations. Apply the values given in the figure.

$\begin{array}{c}I\left({R}_{1}+{R}_{2}+{R}_{3}\right)={V}_{2}-{V}_{1}.\hfill \\ \\ I=\frac{{V}_{2}-{V}_{1}}{{R}_{1}+{R}_{2}+{R}_{3}}=\frac{24\phantom{\rule{0.2em}{0ex}}\text{V}-12\phantom{\rule{0.2em}{0ex}}\text{V}}{10.0\phantom{\rule{0.2em}{0ex}}\text{Ω}+30.0\phantom{\rule{0.2em}{0ex}}\text{Ω}+10.0\phantom{\rule{0.2em}{0ex}}\text{Ω}}=0.20\phantom{\rule{0.2em}{0ex}}\text{A}.\hfill \end{array}$

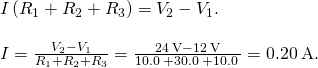
Significance The power dissipated or consumed by the circuit equals the power supplied to the circuit, but detect that the current in the battery ${V}_{1}$ is flowing through the battery from the positive final to the negative terminal and consumes power.

$\begin{array}{}\\ \\ {P}_{{R}_{1}}={I}^{2}{R}_{1}=0.40\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ {P}_{{R}_{2}}={I}^{2}{R}_{2}=1.20\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ {P}_{{R}_{3}}={I}^{2}{R}_{3}=0.80\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ {P}_{{V}_{1}}=I{V}_{1}=2.40\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ {P}_{\text{dissipated}}=4.80\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \\ {P}_{\text{source}}=I{V}_{2}=4.80\phantom{\rule{0.2em}{0ex}}\text{W}\hfill \end{array}$

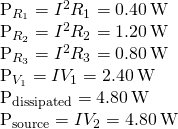
The ability supplied equals the ability dissipated by the resistors and consumed by the battery ${V}_{1}.$

Cheque Your Agreement When using Kirchhoff's laws, you need to decide which loops to utilise and the management of electric current flow through each loop. In analyzing the circuit in (Figure), the direction of current flow was called to be clockwise, from point a to point b. How would the results modify if the direction of the electric current was chosen to be counterclockwise, from betoken b to indicate a?

The current calculated would be equal to $I=-0.20\phantom{\rule{0.2em}{0ex}}\text{A}$ instead of $I=0.20\phantom{\rule{0.2em}{0ex}}\text{A}.$ The sum of the power dissipated and the power consumed would still equal the power supplied.

Multiple Voltage Sources

Many devices crave more than one battery. Multiple voltage sources, such equally batteries, can be connected in series configurations, parallel configurations, or a combination of the two.

In series, the positive concluding of one battery is continued to the negative last of some other battery. Whatsoever number of voltage sources, including batteries, can be connected in serial. Ii batteries connected in series are shown in (Effigy). Using Kirchhoff's loop rule for the circuit in part (b) gives the upshot

$\begin{array}{c}{\epsilon }_{1}-I{r}_{1}+{\epsilon }_{2}-I{r}_{2}-IR=0,\hfill \\ \left[\left({\epsilon }_{1}+{\epsilon }_{2}\right)-I\left({r}_{1}+{r}_{2}\right)\right]-IR=0.\hfill \end{array}$

(a) Two batteries connected in serial with a load resistor. (b) The circuit diagram of the two batteries and the load resistor, with each battery modeled as an arcadian emf source and an internal resistance.

Part a shows two batteries connected in series to a resistor. Part b shows the circuit diagram for part a, with each battery represented by an emf source and internal resistance.

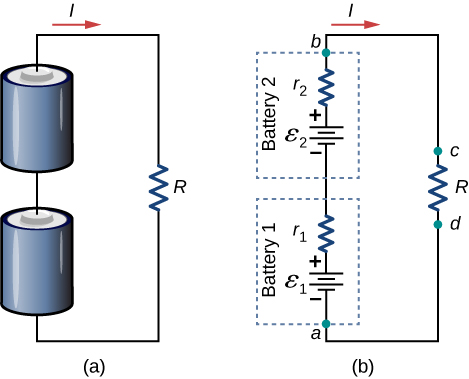
When voltage sources are in series, their internal resistances can be added together and their emfs can be added together to get the total values. Serial connections of voltage sources are common—for example, in flashlights, toys, and other appliances. Normally, the cells are in serial in guild to produce a larger full emf. In (Figure), the terminal voltage is

${V}_{\text{terminal}}=\left({\epsilon }_{1}-I{r}_{1}\right)+\left({\epsilon }_{2}-I{r}_{2}\right)=\left[\left({\epsilon }_{1}+{\epsilon }_{2}\right)-I\left({r}_{1}+{r}_{2}\right)\right]=\left({\epsilon }_{1}+{\epsilon }_{2}\right)+I{r}_{\text{eq}}.$

Annotation that the same electric current I is plant in each bombardment because they are connected in serial. The disadvantage of series connections of cells is that their internal resistances are additive.

Batteries are continued in series to increase the voltage supplied to the circuit. For case, an LED flashlight may have two AAA prison cell batteries, each with a terminal voltage of 1.5 V, to provide three.0 V to the flashlight.

Any number of batteries can be connected in series. For N batteries in serial, the terminal voltage is equal to

${V}_{\text{terminal}}=\left({\epsilon }_{1}+{\epsilon }_{2}+\text{⋯}+{\epsilon }_{N-1}+{\epsilon }_{N}\right)-I\left({r}_{1}+{r}_{2}+\text{⋯}+{r}_{N-1}+{r}_{N}\right)=\sum _{i=1}^{N}{\epsilon }_{i}-I{r}_{\text{eq}}$

where the equivalent resistance is ${r}_{\text{eq}}=\sum _{i=1}^{N}{r}_{i}$ .

When a load is placed across voltage sources in series, equally in (Figure), we can find the current:

$\begin{array}{c}\left({\epsilon }_{1}-I{r}_{1}\right)+\left({\epsilon }_{2}-I{r}_{2}\right)=IR,\hfill \\ I{r}_{1}+I{r}_{2}+IR={\epsilon }_{1}+{\epsilon }_{2},\hfill \\ I=\frac{{\epsilon }_{1}+{\epsilon }_{2}}{{r}_{1}+{r}_{2}+R}.\hfill \end{array}$

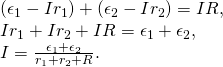
As expected, the internal resistances increase the equivalent resistance.

2 batteries connect in serial to an LED bulb, every bit institute in a flashlight.

Part a shows two batteries connected in series to a bulb. Part b shows the circuit diagram for part a, with each battery represented by an emf source and internal resistance and the bulb represented by a load resistor.

Voltage sources, such equally batteries, can likewise be connected in parallel. (Figure) shows two batteries with identical emfs in parallel and continued to a load resistance. When the batteries are connect in parallel, the positive terminals are connected together and the negative terminals are connected together, and the load resistance is continued to the positive and negative terminals. Normally, voltage sources in parallel have identical emfs. In this uncomplicated instance, since the voltage sources are in parallel, the total emf is the same as the individual emfs of each battery.

(a) Two batteries connect in parallel to a load resistor. (b) The circuit diagram shows the shows battery equally an emf source and an internal resistor. The 2 emf sources have identical emfs (each labeled by $\epsilon$ ) connected in parallel that produce the same emf.

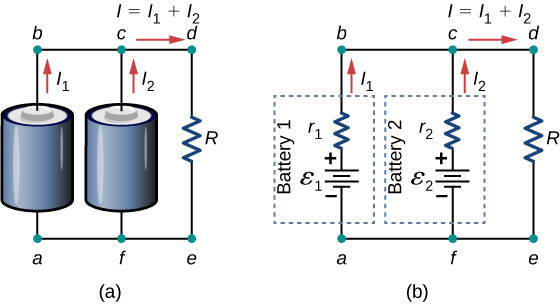
Part a shows two batteries connected in parallel to a resistor. Part b shows the circuit diagram for part a, with each battery represented by an emf source and internal resistance.

Consider the Kirchhoff analysis of the excursion in (Figure)(b). There are two loops and a node at indicate b and $\epsilon ={\epsilon }_{1}={\epsilon }_{2}$ .

Node b: ${I}_{1}+{I}_{2}-I=0$ .

Loop abcfa: $\begin{array}{ccc}\hfill \epsilon -{I}_{1}{r}_{1}+{I}_{2}{r}_{2}-\epsilon & =\hfill & 0,\hfill \\ \hfill {I}_{1}{r}_{1}& =\hfill & {I}_{2}{r}_{2}.\hfill \end{array}$

Loop fcdef: $\begin{array}{ccc}\hfill {\epsilon }_{2}-{I}_{2}{r}_{2}-IR& =\hfill & 0,\hfill \\ \hfill \epsilon -{I}_{2}{r}_{2}-IR& =\hfill & 0.\hfill \end{array}$

Solving for the current through the load resistor results in $I=\frac{\epsilon }{{r}_{\text{eq}}+R}$ , where ${r}_{\text{eq}}={\left(\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}}\right)}^{-1}$ . The terminal voltage is equal to the potential drop across the load resistor $IR=\left(\frac{\epsilon }{{r}_{\text{eq}}+R}\right)$ . The parallel connexion reduces the internal resistance and thus tin can produce a larger electric current.

Any number of batteries can be connected in parallel. For N batteries in parallel, the concluding voltage is equal to

${V}_{\text{terminal}}=\epsilon -I{\left(\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}}+\text{⋯}+\frac{1}{{r}_{N-1}}+\frac{1}{{r}_{N}}\right)}^{-1}=\epsilon -I{r}_{\text{eq}}$

where the equivalent resistance is ${r}_{\text{eq}}={\left(\sum _{i=1}^{N}\frac{1}{{r}_{i}}\right)}^{-1}$ .

As an instance, some diesel fuel trucks use two 12-V batteries in parallel; they produce a total emf of 12 V just tin can deliver the larger electric current needed to offset a diesel engine.

In summary, the terminal voltage of batteries in serial is equal to the sum of the individual emfs minus the sum of the internal resistances times the current. When batteries are connected in parallel, they usually accept equal emfs and the last voltage is equal to the emf minus the equivalent internal resistance times the current, where the equivalent internal resistance is smaller than the individual internal resistances. Batteries are connected in series to increase the last voltage to the load. Batteries are connected in parallel to increase the current to the load.

Solar Prison cell Arrays

Another example dealing with multiple voltage sources is that of combinations of solar cells—wired in both series and parallel combinations to yield a desired voltage and current. Photovoltaic generation, which is the conversion of sunlight directly into electricity, is based upon the photoelectric effect. The photoelectric effect is beyond the telescopic of this chapter and is covered in Photons and Matter Waves, merely in full general, photons hitting the surface of a solar cell create an electric electric current in the cell.

Well-nigh solar cells are fabricated from pure silicon. Most single cells take a voltage output of virtually 0.v V, while the current output is a role of the amount of sunlight falling on the cell (the incident solar radiations known as the insolation). Nether bright noon sunlight, a current per unit area of about $100{\phantom{\rule{0.2em}{0ex}}\text{mA/cm}}^{2}$ of jail cell surface expanse is produced by typical single-crystal cells.

Individual solar cells are connected electrically in modules to meet electric energy needs. They tin be wired together in series or in parallel—continued similar the batteries discussed earlier. A solar-prison cell array or module normally consists of between 36 and 72 cells, with a power output of 50 Westward to 140 Due west.

Solar cells, like batteries, provide a directly electric current (dc) voltage. Electric current from a dc voltage source is unidirectional. Well-nigh household appliances demand an alternating current (air conditioning) voltage.

Summary

Kirchhoff'southward rules can be used to analyze whatsoever excursion, simple or complex. The simpler series and parallel connection rules are special cases of Kirchhoff'due south rules.
Kirchhoff's first rule, too known equally the junction rule, applies to the accuse to a junction. Current is the flow of charge; thus, whatever accuse flows into the junction must menstruation out.
Kirchhoff's second rule, also known as the loop rule, states that the voltage drop around a loop is zip.
When computing potential and electric current using Kirchhoff's rules, a set up of conventions must be followed for determining the correct signs of various terms.
When multiple voltage sources are in series, their internal resistances add together and their emfs add together to get the total values.
When multiple voltage sources are in parallel, their internal resistances combine to an equivalent resistance that is less than the individual resistance and provides a higher electric current than a unmarried prison cell.
Solar cells tin can exist wired in serial or parallel to provide increased voltage or current, respectively.

Conceptual Questions

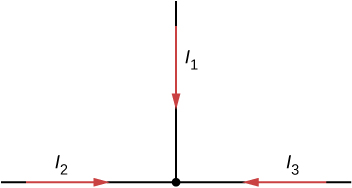
Can all of the currents going into the junction shown below be positive? Explain.

The figure shows a junction with three incoming current branches.

Consider the circuit shown below. Does the analysis of the excursion require Kirchhoff's method, or can it be redrawn to simplify the excursion? If it is a circuit of series and parallel connections, what is the equivalent resistance?

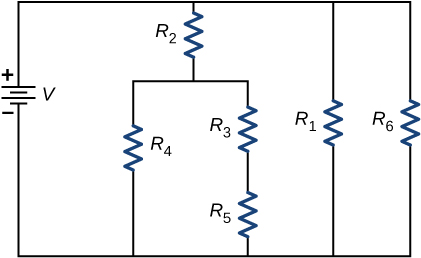
The figure shows a circuit with positive terminal of voltage source V connected to three parallel branches. The first branch has resistor R subscript 2 connected to parallel branches with R subscript 4 and R subscript 3 series with R subscript 5. The second branch has resistor R subscript 1 and third branch has resistor R subscript 6.

It can be redrawn.
${R}_{\text{eq}}={\left[\frac{1}{{R}_{6}}+\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}+{\left(\frac{1}{{R}_{4}}+\frac{1}{{R}_{3}+{R}_{5}}\right)}^{-1}}\right]}^{-1}$

Practice batteries in a excursion ever supply ability to a excursion, or can they blot power in a circuit? Requite an example.

What are the advantages and disadvantages of connecting batteries in series? In parallel?

In series the voltages add, but so do the internal resistances, considering the internal resistances are in series. In parallel, the terminal voltage is the aforementioned, but the equivalent internal resistance is smaller than the smallest individual internal resistance and a higher current tin can be provided.

Semi-tractor trucks use four large 12-5 batteries. The starter system requires 24 V, while normal functioning of the truck's other electrical components utilizes 12 5. How could the four batteries be continued to produce 24 V? To produce 12 5? Why is 24 V improve than 12 5 for starting the truck's engine (a very heavy load)?

Issues

Consider the circuit shown below. (a) Notice the voltage across each resistor. (b)What is the power supplied to the circuit and the power prodigal or consumed past the circuit?

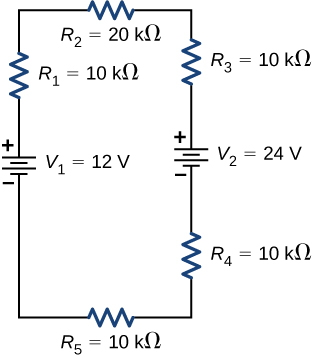
Consider the circuits shown below. (a) What is the current through each resistor in part (a)? (b) What is the current through each resistor in part (b)? (c) What is the power dissipated or consumed by each circuit? (d) What is the power supplied to each circuit?

a. ${I}_{1}=0.6\phantom{\rule{0.2em}{0ex}}\text{mA},\phantom{\rule{0.5em}{0ex}}{I}_{2}=0.4\phantom{\rule{0.2em}{0ex}}\text{mA},\phantom{\rule{0.5em}{0ex}}{I}_{3}=0.2\phantom{\rule{0.2em}{0ex}}\text{mA}$ ;
b. ${I}_{1}=0.04\phantom{\rule{0.2em}{0ex}}\text{mA},\phantom{\rule{0.5em}{0ex}}{I}_{2}=1.52\phantom{\rule{0.2em}{0ex}}\text{mA},\phantom{\rule{0.5em}{0ex}}{I}_{3}=-1.48\phantom{\rule{0.2em}{0ex}}\text{mA}$ ; c. ${P}_{\text{out}}=0.92\phantom{\rule{0.2em}{0ex}}\text{mW},\phantom{\rule{0.5em}{0ex}}{P}_{\text{out}}=4.50\phantom{\rule{0.2em}{0ex}}\text{mW}$ ;
d. ${P}_{\text{in}}=0.92\phantom{\rule{0.2em}{0ex}}\text{mW},\phantom{\rule{0.5em}{0ex}}{P}_{\text{in}}=4.50\phantom{\rule{0.2em}{0ex}}\text{mW}$

Consider the excursion shown below. Observe ${V}_{1},{I}_{2},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{I}_{3}.$

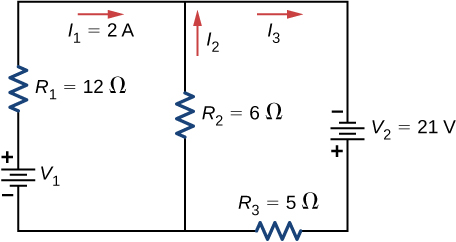
The positive terminal of voltage source V subscript 1 is connected to resistance R subscript 1 of 12 Ω with right current I subscript 1 of 2 A connected to two parallel branches, first with resistor R subscript 2 of 6 Ω with upward current I subscript 2 and second with right current I subscript 3, negative terminal of voltage source V subscript 2 of 21 V and resistor R subscript 3 of 5 Ω.

Consider the circuit shown below. Find ${V}_{1},{V}_{2},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{R}_{4}.$

${V}_{1}=42\phantom{\rule{0.2em}{0ex}}\text{V},{V}_{2}=6\phantom{\rule{0.2em}{0ex}}\text{V},{R}_{4}=18\phantom{\rule{0.2em}{0ex}}\text{Ω}$

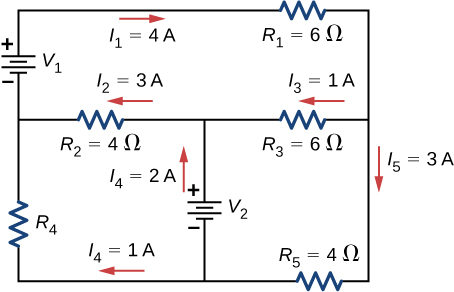
Consider the excursion shown below. Find ${I}_{1},{I}_{2},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{I}_{3}.$

Consider the circuit shown below. (a) Find ${I}_{1},{I}_{2},{I}_{3},{I}_{4},\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{I}_{5}.$ (b) Find the power supplied by the voltage sources. (c) Find the ability prodigal by the resistors.

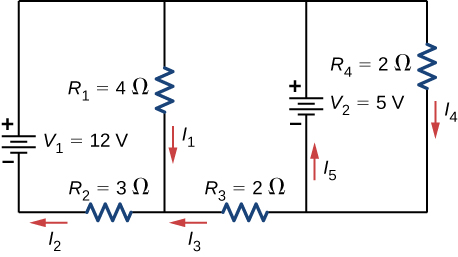
a. ${I}_{1}=1.5\phantom{\rule{0.2em}{0ex}}\text{A},{I}_{2}=2\phantom{\rule{0.2em}{0ex}}\text{A},{I}_{3}=0.5\phantom{\rule{0.2em}{0ex}}\text{A},\phantom{\rule{0.2em}{0ex}}{I}_{4}=2.5\phantom{\rule{0.2em}{0ex}}\text{A},{I}_{5}=2\phantom{\rule{0.2em}{0ex}}\text{A}$ ; b. ${P}_{\text{in}}={I}_{2}{V}_{1}+{I}_{5}{V}_{5}=34\phantom{\rule{0.2em}{0ex}}\text{W}$ ;
c. ${P}_{\text{out}}={I}_{1}^{2}{R}_{1}+{I}_{2}^{2}{R}_{2}+{I}_{3}^{2}{R}_{3}+{I}_{4}^{2}{R}_{4}=34\phantom{\rule{0.2em}{0ex}}\text{W}$

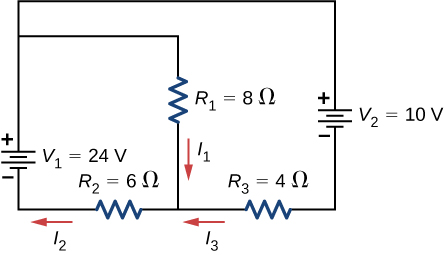
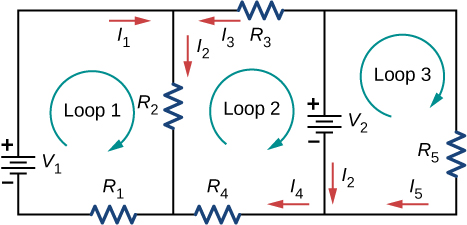
Consider the circuit shown below. Write the 3 loop equations for the loops shown.

Consider the circuit shown below. Write equations for the iii currents in terms of R and V.

${I}_{1}=\frac{2}{3}\frac{V}{R},{I}_{2}=\frac{V}{3R},{I}_{3}=\frac{V}{3R}$

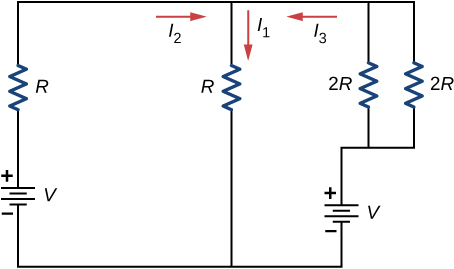
Consider the circuit shown in the preceding trouble. Write equations for the power supplied by the voltage sources and the power dissipated by the resistors in terms of R and V.

A child'southward electronic toy is supplied past three i.58-V alkaline cells having internal resistances of $0.0200\phantom{\rule{0.2em}{0ex}}\text{Ω}$ in series with a i.53-V carbon-zinc dry cell having a $0.100\text{-}\text{Ω}$ internal resistance. The load resistance is $10.0\phantom{\rule{0.2em}{0ex}}\text{Ω}$ . (a) Describe a circuit diagram of the toy and its batteries. (b) What electric current flows? (c) How much ability is supplied to the load? (d) What is the internal resistance of the dry prison cell if it goes bad, resulting in only 0.500 W being supplied to the load?

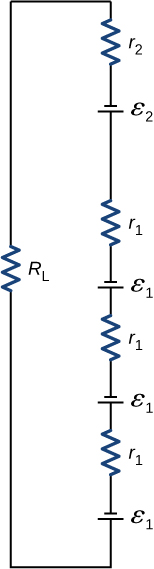
The resistor R subscript L is connected in series with resistor r subscript 2, voltage source ε subscript 2, resistor r subscript 1, voltage source ε subscript 1, resistor r subscript 1, voltage source ε subscript 1, resistor r subscript 1and voltage source ε subscript 1. All voltage sources have upward negative terminals.

;
b. 0.617 A; c. three.81 W; d. $18.0\phantom{\rule{0.2em}{0ex}}\text{Ω}$

Apply the junction rule to Junction b shown beneath. Is whatsoever new information gained by applying the junction rule at east?

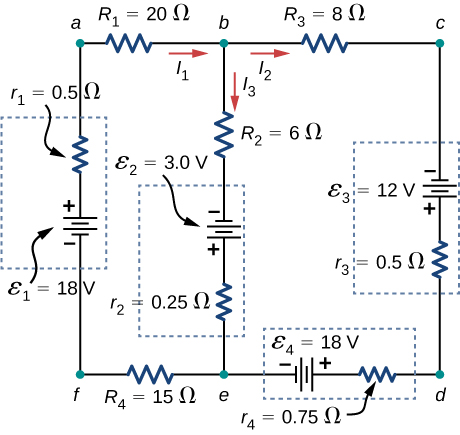
Apply the loop rule to Loop afedcba in the preceding problem.

${I}_{1}{r}_{1}-{\epsilon }_{1}+{I}_{1}{R}_{4}+{\epsilon }_{4}+{I}_{2}{r}_{4}+{I}_{4}{r}_{3}-{\epsilon }_{3}+{I}_{2}{R}_{3}+{I}_{1}{R}_{1}=0$

Glossary

junction rule: sum of all currents entering a junction must equal the sum of all currents leaving the junction

Kirchhoff's rules: set of 2 rules governing current and changes in potential in an electric excursion

loop rule: algebraic sum of changes in potential around any closed circuit path (loop) must be zero

marchantallis1956.blogspot.com

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/kirchhoffs-rules/

How Do You Know When a Resistor Is Redundant

64 Kirchhoff'southward Rules

Learning Objectives

Kirchhoff's Kickoff Rule

Kirchhoff's Second Rule

Applying Kirchhoff'due south Rules

Multiple Voltage Sources

Solar Prison cell Arrays

Summary

Conceptual Questions

Issues

Glossary

0 Response to "How Do You Know When a Resistor Is Redundant"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel